23  Overlapping density plot

This graph is largely complete and just needs final proof reading.

This graph requires:

✅ a categorical variable

✅ a numeric (continuous) variable

23.1 Description

Density plots are smoothed version(s) of histogram(s). They can are great for comparing the distributions of a continuous variable across the levels of a categorical variable.

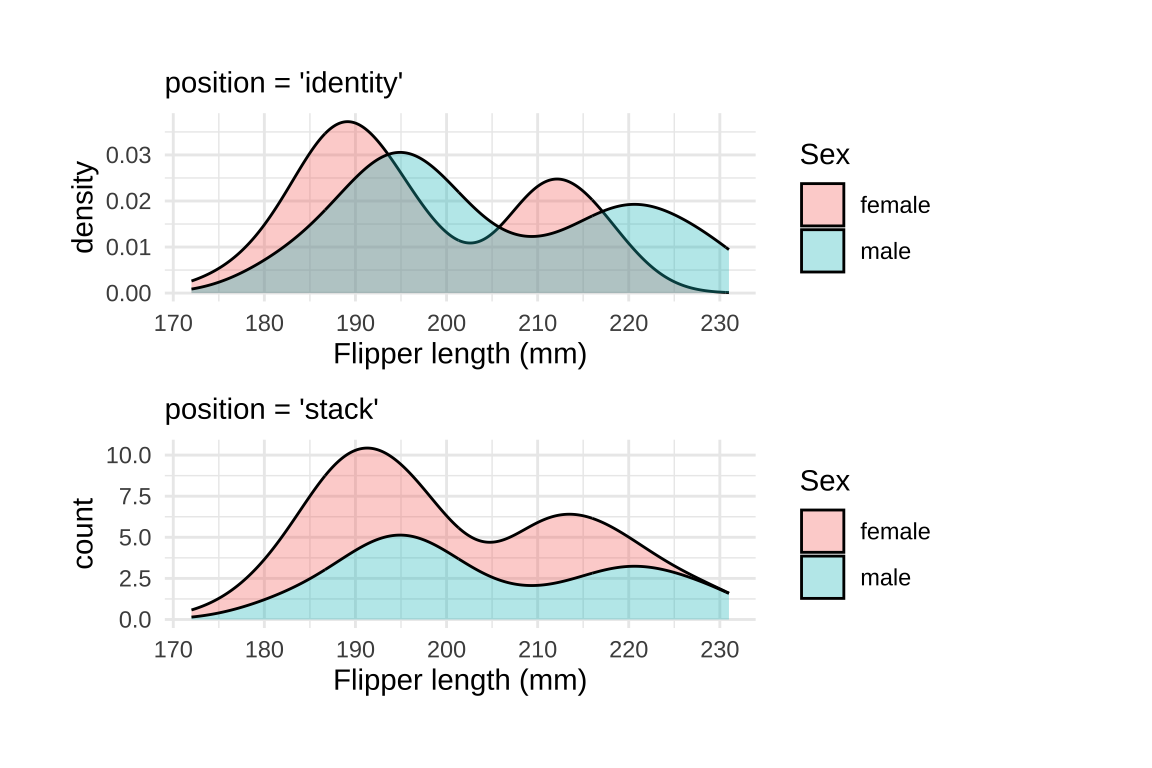
geom_density() creates a kernel density estimate. The default position argument is "identity", which takes the data as is. However, we can change position to "stack" to display overlapping distributions.

23.2 Set up

PACKAGES:

Install packages.

install.packages("palmerpenguins")
library(palmerpenguins)
library(ggplot2)

DATA:

Artwork by allison horst

Remove missing sex from the penguins data

peng_density <- dplyr::filter(penguins, !is.na(sex))
dplyr::glimpse(peng_density)
#> Rows: 333
#> Columns: 8
#> $ species           <fct> Adelie, Adelie, Adelie…
#> $ island            <fct> Torgersen, Torgersen, …
#> $ bill_length_mm    <dbl> 39.1, 39.5, 40.3, 36.7…
#> $ bill_depth_mm     <dbl> 18.7, 17.4, 18.0, 19.3…
#> $ flipper_length_mm <int> 181, 186, 195, 193, 19…
#> $ body_mass_g       <int> 3750, 3800, 3250, 3450…
#> $ sex               <fct> male, female, female, …
#> $ year              <int> 2007, 2007, 2007, 2007…

23.3 Grammar

CODE:

• Create labels with labs()

• Initialize the graph with ggplot() and provide data

• Map the flipper_length_mm to the x and sex to fill

• Add the geom_density()

• Set the alpha to 1/3 (to handle the overlapping areas)

labs_ovrlp_density <- labs(
  title = "Adult foraging penguins",
  x = "Flipper length (millimeters)",
  fill = "Sex")
ggp2_ovrlp_density <- ggplot(data = peng_density, 
       aes(x = flipper_length_mm, 
           fill = sex)) +
      geom_density(alpha = 1/3) 
ggp2_ovrlp_density + 
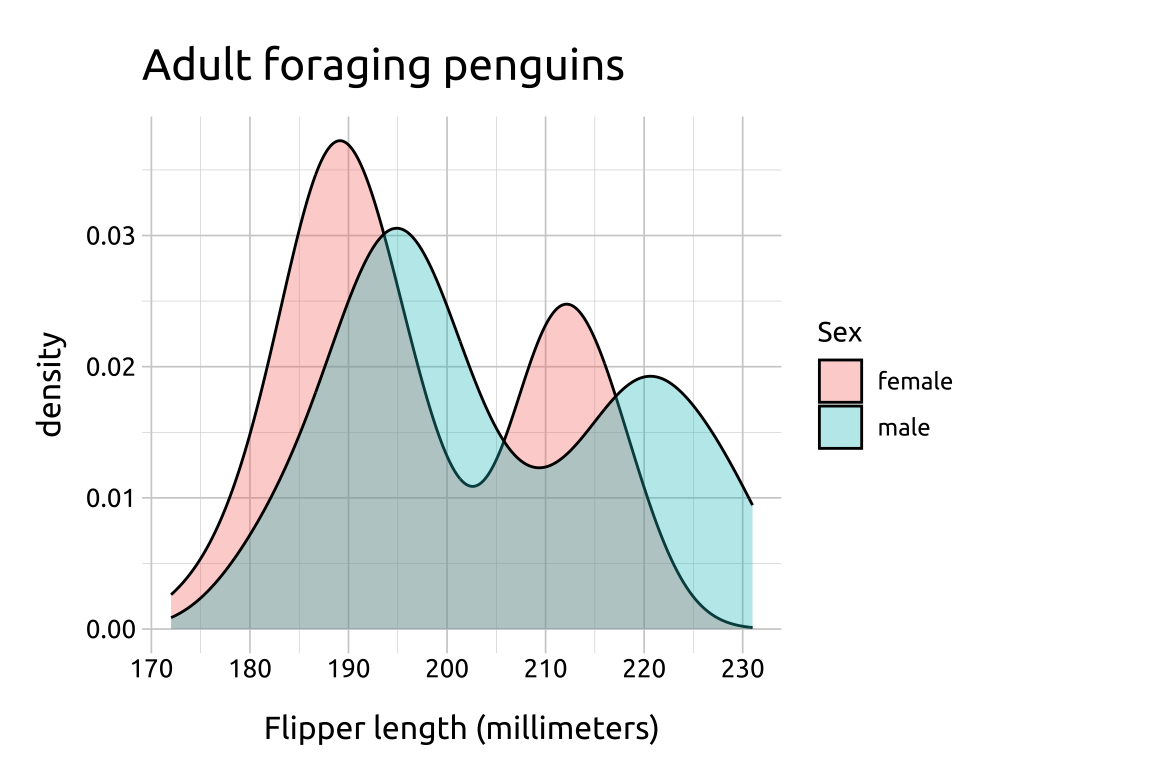
  labs_ovrlp_density

GRAPH:

A downside of density plots is the lack of interpretability of the y axis

Make density area slightly transparent to handle over-plotting.

23.4 More info

ggplot2 has multiple options for overlapping density plots, so which one to use will depend on how you’d like to display the relative distributions in your data. We’ll cover three options below:

23.4.1 "stack"

If we change the position to "stack" we can see the smoothed estimates are ‘stacked’ on top each other (and the y axis shifts slightly).

labs_stack_density <- labs(
    title = "Adult foraging penguins",
    x = "Flipper length (millimeters)",
    fill = "Sex")
ggp2_stack_density <- ggplot(data = peng_density,
    mapping = aes(x = flipper_length_mm,
               fill = sex)) +
    geom_density(position = "stack",
                 alpha = 1 / 3)
ggp2_stack_density +
    labs_stack_density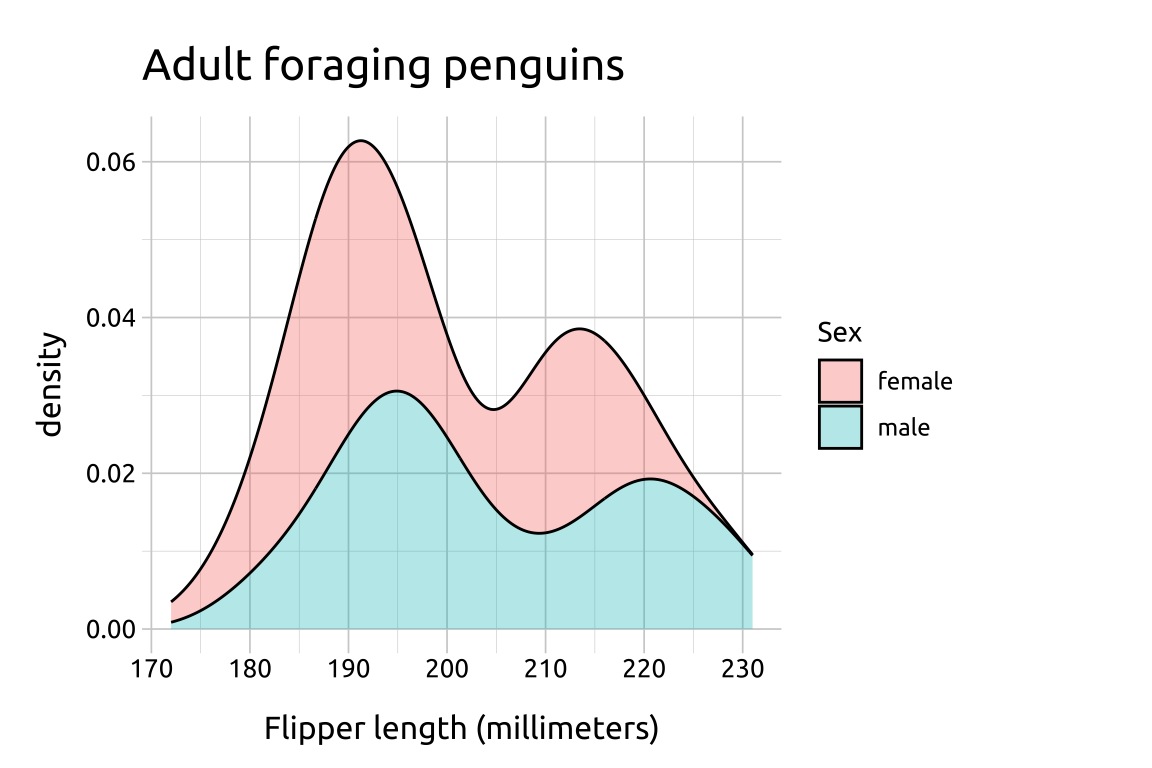

Setting position to 'stack' loses marginal densities

23.4.2 after_stat(count)

If we include after_stat(count) as one of our mapped aesthetics, the mapping is postponed until after statistical transformation, and uses the density * n instead of the default density.

labs_after_stat_density <- labs(
  title = "Adult foraging penguins",
  x = "Flipper length (millimeters)", 
  fill = "Sex")
ggp2_after_stat_density <- ggplot(data = peng_density, 
       aes(x = flipper_length_mm, 
           after_stat(count),
           fill = sex)) +
      geom_density(position = "stack", 
                   alpha = 1/3) 
ggp2_after_stat_density + 
  labs_after_stat_density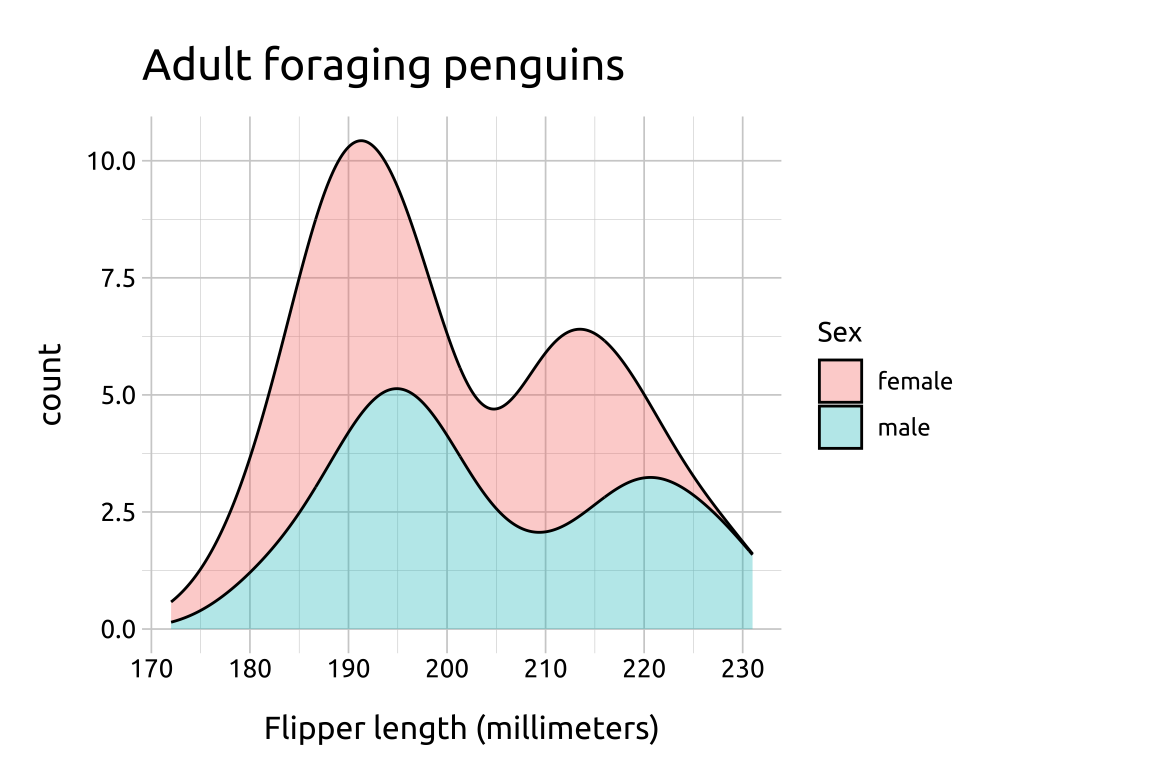

Adding after_stat(count) ‘preserves marginal densities.’, which result in more a interpretable y axis (depending on the audience)

23.4.3 "fill"

Using after_stat(count) with position = "fill" creates in a conditional density estimate.

labs_fill_density <- labs(
  title = "Adult foraging penguins",
  x = "Flipper length (millimeters)", 
  fill = "Sex")
ggp2_fill_density <- ggplot(data = peng_density, 
       aes(x = flipper_length_mm, 
           after_stat(count),
           fill = sex)) +
      geom_density(position = "fill", 
                   alpha = 1/3) 
ggp2_fill_density + 
  labs_fill_density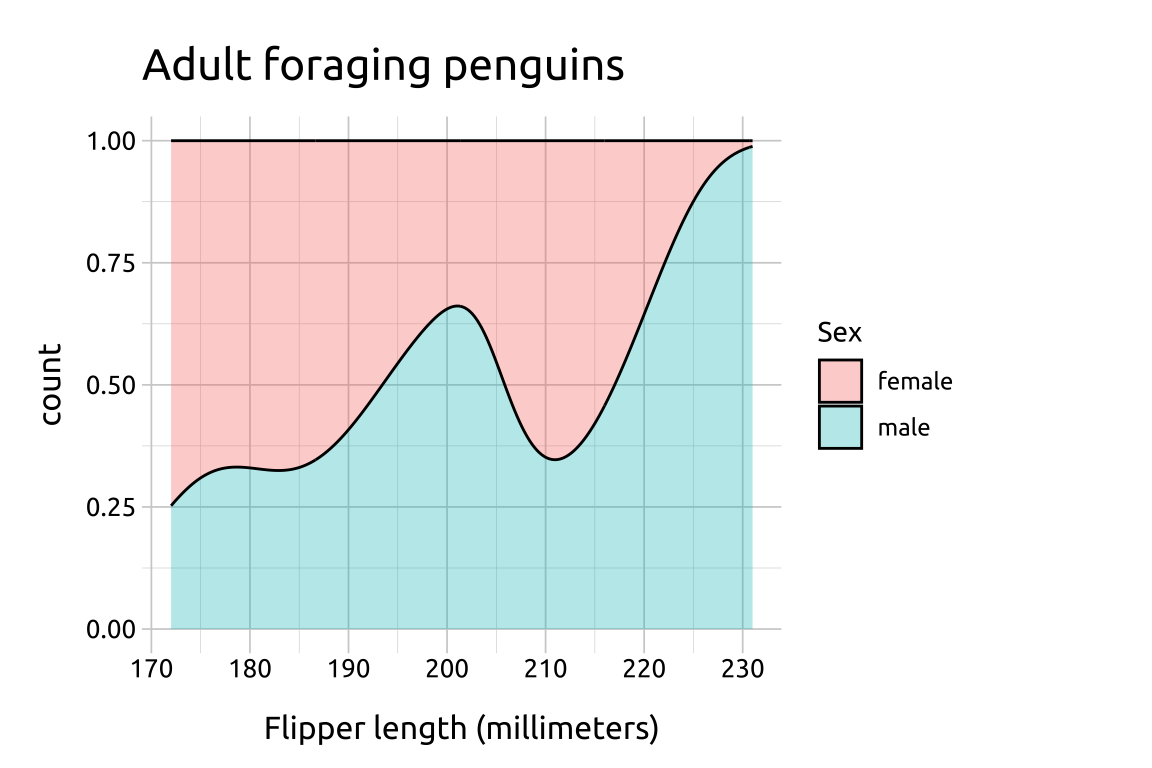

This results in a y axis ranging from 0-1, and the area filled with the relative proportional values.